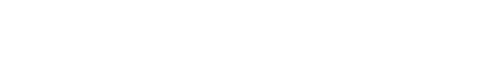今回は、得点と勝利の関係について解析してみます。
参考は例によって偉大なる著書
Rによるセイバーメトリクス入門です。
得点と勝利の関係について
すべてのスポーツの目標は、試合に勝つことです。
野球において勝利とは、相手より多くの点を取ることに尽きます。
その中で、自チームが取った得点 と 自チームが取られた得点
は大きく勝敗に影響を与えると言われています。
今回は、実際に計算をしてみようと思います。
Lahman Databaseからの抽出
Lahmanのデータベースにはチームの情報が入っています。
library(Lahman)この中のTeamsの情報について見てみます。
tail(Teams, 3)yearID lgID teamID franchID divID Rank G Ghome W L DivWin WCWin LgWin
2983 2021 AL TEX TEX W 5 162 81 60 102 N N N
2984 2021 AL TOR TOR E 4 162 80 91 71 N N N
2985 2021 NL WAS WSN E 5 162 81 65 97 N N N
head(Teams, 3)
earID lgID teamID franchID divID Rank G Ghome W L DivWin WCWin LgWin WSWin
1 1871 NA BS1 BNA <NA> 3 31 NA 20 10 <NA> <NA> N <NA>
2 1871 NA CH1 CNA <NA> 2 28 NA 19 9 <NA> <NA> N <NA>
3 1871 NA CL1 CFC <NA> 8 29 NA 10 19 <NA> <NA> N <NA>
これによって1871年から2021年までのチームデータがあることがわかります。
このデータを扱って行きましょう。
2000年以降で、短縮シーズンだった2020年を除くデータを取り出します。
my_teams <- Teams %>%
filter(yearID != 2020 & yearID>2000)%>%
select(teamID, yearID, lgID, G, W,L,R,RA)
続いて、得失点差RDと勝率Wpctを算出します。
my_teams<- my_teams%>%
mutate(RD = R-RA, Wpct = W/(W+L))
そうしたら、得失点差と勝利をプロットしてみます。
run_diff <- ggplot(my_teams, aes(x = RD, y = Wpct))+
geom_point()+
scale_x_continuous("Run differential")+
scale_y_continuous("Winning percentage")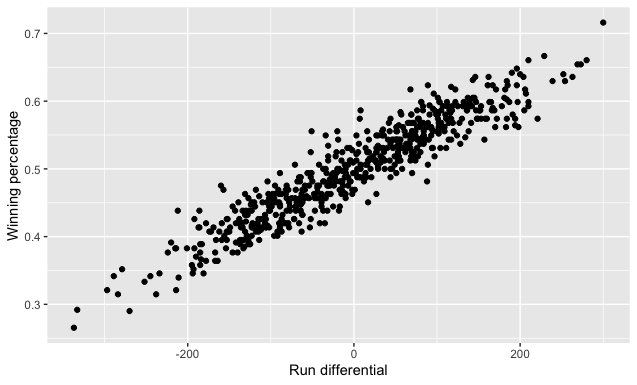
そうすると、、、
得失点差と勝率には関連があるようなグラフになりましたね!
得点が+200点ぐらいだと、勝率は0.600ぐらいです。
MLBの場合、162試合ありますので、
勝率0.6 だと97勝ぐらいになります。
線形回帰
過去の傾向から、チームの勝率を予測するモデルを作成します。
ここでは線形モデルとします
勝率 = a + b×得失点差 + ε
この関数を求めます。
crcblue<- "#2905A1"
linfit <- lm(Wpct ~ RD, data = my_teams) そうすると、
Call:
lm(formula = Wpct ~ RD, data = my_teams)
Coefficients:
(Intercept) RD
0.4999888 0.0006143
とうい結果になり、
勝率 = 0.4999888 + 0.0006143×得失点差
と表せられます。
得失点が0点の場合、勝率は0.4999
+1点となるにつれてちょっとずつ勝率が上がります。
グラフ化するとこのようになります。
線形に回帰されるとしても、基準から外れる値はあります。
そのチームについて調べてみます。
実データと線形モデルの差=残差をもとめます。
my_team_aug<-augment(linfit, data = my_teams) 得失点差と残差についてのグラフを作成します。
base_plot <- ggplot(my_team_aug, aes(x = RD, y=.resid))+
geom_point(alpha = 0.3)+
geom_hline(yintercept = 0, linetyep =3)+
xlab("Run differential") + ylab("Residual")ここで、残差が多い順に(モデルからかけ離れている順に)抽出します。
highlight_teams<- my_team_aug%>%
arrange(desc(abs(.resid)))%>%
head(6)teamID yearID lgID G W L R RA RD Wpct .fitted .resid
<fct> <int> <fct> <int> <int> <int> <int> <int> <int> <dbl> <dbl> <dbl>
1 SEA 2021 AL 162 90 72 697 748 -51 0.556 0.469 0.0869
2 TEX 2016 AL 162 95 67 765 757 8 0.586 0.505 0.0815
3 LAA 2008 AL 162 100 62 765 697 68 0.617 0.542 0.0755
4 ARI 2005 NL 162 77 85 696 856 -160 0.475 0.402 0.0736
5 CLE 2006 AL 162 78 84 870 782 88 0.481 0.554 -0.0726
6 SEA 2018 AL 162 89 73 677 711 -34 0.549 0.479 0.0703
これをグラフ化します
base_plot+
geom_point(data = highlight_teams, color= crcblue)+
geom_text_repel(data = highlight_teams,color = crcblue,
aes(label = paste(teamID, yearID)))
非常に面白い図となりました!
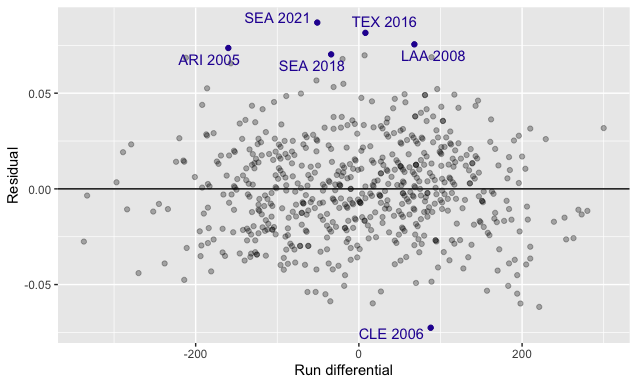
このグラフを解説すると、
その得失点差で予測される勝率 との差になります
0より大きいと、予測される勝率より、その数字分勝率が上回ったことを示します。
そうすると、2021年のマリナーズが一番頑張ったことを示します。
この年は大躍進だったみたいですね。
このように、得失点差を利用すると
勝率を大方予想できるみたいです。